Método de aceptación y rechazo

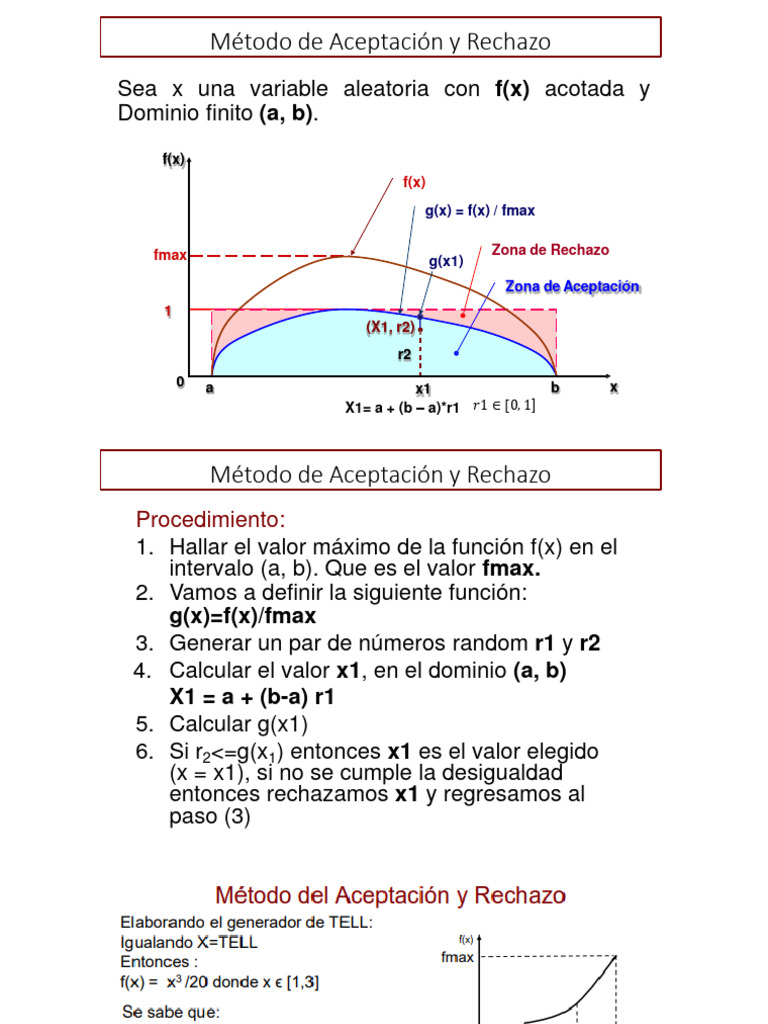
El método de aceptación y rechazo es un algoritmo para generar números pseudoaleatorios provenientes de una variable aleatoria.

Descripción

Sea ${\displaystyle f_{X}(x)}$ la función de densidad de la variable aleatoria ${\displaystyle X}$, supongamos que existe una función ${\displaystyle g(x)}$ tal que

${\displaystyle g(x)\geq f_{X}(x)}$

${\displaystyle \forall \;x\in R_{X}}$ donde ${\displaystyle R_{X}}$ denota el soporte de la variable aleatoria ${\displaystyle X}$, como

${\displaystyle \int _{R_{X}}f_{X}(x)dx=1}$

por ser función de densidad entonces

${\displaystyle \int _{R_{X}}g(x)dx=M\geq 1}$

para que ${\displaystyle g(x)}$ sea una función de densidad, definimos la función

${\displaystyle d(x):={\frac {g(x)}{M}}}$

para ${\displaystyle x\in R_{X}}$ y ${\displaystyle d(x)=0}$ para ${\displaystyle x\notin R_{X}}$.

El método de aceptación y rechazo supone que podemos generar una variable aleatoria ${\displaystyle Y}$ con función de densidad ${\displaystyle d}$.

Algoritmo

El algoritmo para obtener una muestra pseudoaleatoria proveniente de una variable aleatoria ${\displaystyle X}$ con función de densidad ${\displaystyle f}$ utilizando una muestra pseudoaleatoria de una variable aleatoria ${\displaystyle Y}$ con función de densidad ${\displaystyle d}$ es el siguiente:

1. Generar ${\displaystyle Y}$ con función de densidad ${\displaystyle d}$.
2. Generar ${\displaystyle U\sim \operatorname {U} (0,1)}$ independiente de ${\displaystyle Y}$.
3. Si ${\displaystyle U\leq {\frac {f(Y)}{g(Y)}}}$ entonces ${\displaystyle X=Y}$ de lo contrario repetir el paso ${\displaystyle 1}$.

El algoritmo toma en promedio ${\displaystyle M}$ iteraciones para obtener una muestra pseudoaleatoria.

Validez del algoritmo

Para demostrar la validez de este algoritmo veamos que ${\displaystyle \forall \;x\in R_{X}}$ se verifica

${\displaystyle \operatorname {P} [X\leq x]=\int _{-\infty }^{x}f(y)dy}$

Notemos que

${\displaystyle {\begin{aligned}\operatorname {P} [X\leq x]&=\operatorname {P} \left[Y\leq x\;{\bigg |}\;U\leq {\frac {f(Y)}{g(Y)}}\right]\\&={\frac {\displaystyle \operatorname {P} \left[Y\leq x\;,\;U\leq {\frac {f(Y)}{g(Y)}}\right]}{\displaystyle \operatorname {P} \left[U\leq {\frac {f(Y)}{g(Y)}}\right]}}\end{aligned}}}$

pero

${\displaystyle {\begin{aligned}\operatorname {P} \left[Y\leq x\;,\;U\leq {\frac {f(Y)}{g(Y)}}\right]&=\int _{-\infty }^{x}\operatorname {P} \left[Y\leq x\;,\;U\leq {\frac {f(Y)}{g(Y)}}\;{\bigg |}\;Y=y\right]d(y)dy\\&=\int _{-\infty }^{x}\operatorname {P} \left[U\leq {\frac {f(Y)}{g(Y)}}\;{\bigg |}\;Y=y\right]{\frac {g(y)}{M}}\;dy\\&=\int _{-\infty }^{x}\operatorname {P} \left[U\leq {\frac {f(y)}{g(y)}}\right]{\frac {g(y)}{M}}\;dy\\&=\int _{-\infty }^{x}{\frac {f(y)}{g(y)}}{\frac {g(y)}{M}}\;dy\\&={\frac {1}{M}}\int _{-\infty }^{x}f(y)dy\end{aligned}}}$

y

${\displaystyle {\begin{aligned}\operatorname {P} \left[U\leq {\frac {f(Y)}{g(Y)}}\right]&=\int _{R_{Y}}\operatorname {P} \left[U\leq {\frac {f(Y)}{g(Y)}}\;{\bigg |}\;Y=y\right]d(y)dy\\&=\int _{R_{Y}}\operatorname {P} \left[U\leq {\frac {f(y)}{g(y)}}\right]{\frac {g(y)}{M}}\;dy\\&=\int _{R_{Y}}{\frac {f(y)}{g(y)}}{\frac {g(y)}{M}}\;dy\\&={\frac {1}{M}}\int _{R_{Y}}f(y)dy\\&={\frac {1}{M}}\end{aligned}}}$

Por lo tanto

${\displaystyle {\begin{aligned}\operatorname {P} [X\leq x]&={\frac {\operatorname {P} \left[Y\leq x\;,\;U\leq {\frac {f(Y)}{g(Y)}}\right]}{\operatorname {P} \left[U\leq {\frac {f(Y)}{g(Y)}}\right]}}\\&={\frac {\displaystyle {\frac {1}{M}}\int _{-\infty }^{x}f(y)dy}{\displaystyle {\frac {1}{M}}}}\\&=\int _{-\infty }^{x}f(y)dy\end{aligned}}}$

Véase también

• Método de la transformada inversa
• Número pseudoaleatorio
• Generador lineal congruencial

Referencias

• Ross, S.M. (2013). Simulation. Academic Press.
• Law, A.M. (2014) Simulation Modeling and Analysis. McGrawHill.